What is Heteroscedasticity and How do we Test for it ?

Once your linear regression model is trained, you should always plot your residuals (y – ŷ) whether the errors are homoscedastic or heteroscedastic. What do we mean by these terms? It means that there should not be any pattern in residuals and they should be uniformly distributed, or in other words, there should not be any variance in the residuals. Homoscedasticity is one of the assumptions of linear regression, so it is often important to check for it.

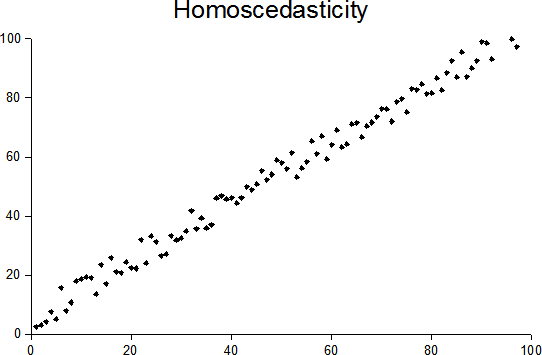
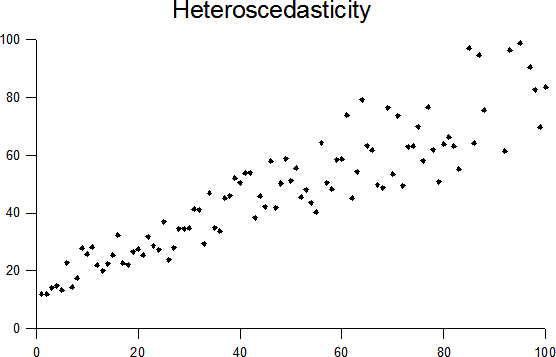
In the above figures, you can clearly see that the residuals have a clear pattern in the heteroscedastic image. In that scenario, you cannot rely on the regression analysis.

How to test for heteroscedasticity?

There are many ways to test for heteroscedasticity, I’ll list a. few ways here –

1. Visual Test – Just look at the residual plot and you’ll often see whether the residuals have any variance or not, not very accurate but often works.
2. Bartlett test
3. Breusch Pagan test
4. Goldfeld Quandt test
5. Glesjer test
6. Test based on Spearman’s rank correlation coefficient
7. White test
8. Ramsey test
9. Harvey Phillips test
10. Szroeter test
11. Peak test (nonparametric) test

All these tests in one way or another try to reject the null hypothesis H₀ : variance is constant and the alternative hypothesis is that H_a : variance is not constant. You can go into detail about the tests here.