ML EXPLAINED

Category: Data Science Interview

  • Daily Coding Problem #1511

    Good morning! Here’s your coding interview problem for today.

    This problem was asked by Google.

    Given a binary search tree and a range [a, b] (inclusive), return the sum of the elements of the binary search tree within the range.

    For example, given the following tree:

        5
   / \
  3   8
 / \ / \
2  4 6  10

    and the range [4, 9], return 23 (5 + 4 + 6 + 8).

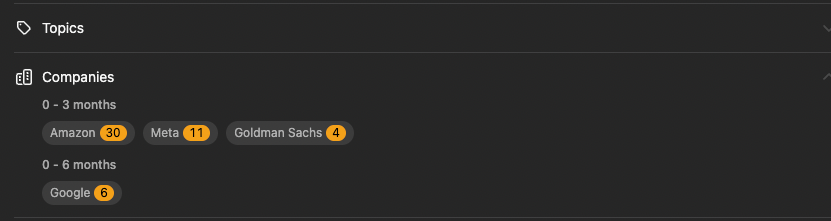
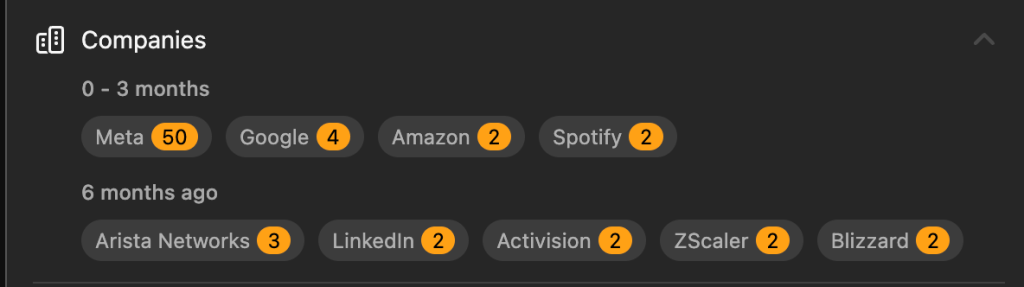
    The problem is also the same as LeetCode 938 and this problem has not only been asked by google but also by meta, and a lot recently.

    The way to approach this problem is to do a pre-order traversal and at each step check whether the value at the node is within the specified range, if it is then we add it to our running sum.

    Now when do you want to go to the left node, it’s only when the value of your node is greater than the lower bound. If the value of your node is lesser than the lower bound, then you don’t want to explore the left sub-tree as all of them will have value lower than the node.

    Again, you only want to explore the right subtree if the value of the current node is less than the upper bound.

    So we call the function recursively on the left subtree if the value of the current node is higher than the lower bound and on the right subtree if the value of the node is lower than the upper bound.

    Here is the solution – 

    class Solution:
    def rangeSumBST(self, root: Optional[TreeNode], low: int, high: int) -> int:
        if not root:
            return 0

        self.range_sum = 0
        self.dfs(root,low,high)
        return self.range_sum

    def dfs(self,node,low,high):
        if not node:
            return 0

        if low <=node.val<=high:
            self.range_sum+=node.val
        
        if node.val > low:
            self.dfs(node.left,low,high)

        if node.val < high:
            self.dfs(node.right,low,high)

    Both time and space complexity is O(N) cause we are exploring all the nodes in the worse case and the recursive call stack takes up O(N) space.

  • LeetCode 1249 – Minimum Remove To Make Valid Parentheses

    This is one of the most asked questions by Meta in the past 3 months.

    Given a string s of '(' , ')' and lowercase English characters.

    Your task is to remove the minimum number of parentheses ( '(' or ')', in any positions ) so that the resulting parentheses string is valid and return any valid string.

    Formally, a parentheses string is valid if and only if:

    • It is the empty string, contains only lowercase characters, or
    • It can be written as AB (A concatenated with B), where A and B are valid strings, or
    • It can be written as (A), where A is a valid string.

    Example 1:

    Input: s = "lee(t(c)o)de)"
    Output: "lee(t(c)o)de"
    Explanation: "lee(t(co)de)" , "lee(t(c)ode)" would also be accepted.

    The way to solve the problem is by using a combination of stack and a set.

    You iterate through the string and check if the parentheses is valid with the help of a stack, as you do in the easy question Valid Parentheses. If you come across an invalid one, then you add the index to your set which tracks which indices to remove.

    In the example lee(t(c)o)de) , we will initialise our stack to be empty and iterate through the array. Once we encounter a parenthesis, we check if its a closing or opening one. So we go through l,e,e, and we now have (, so we add the index to the stack. Our stack becomes [3], we continue and keep adding to the stack if it’s an open, otherwise we pop from the stack.

    So our stack is [3,5] when we are at lee(t(c, now we see two closing brackets, so we pop twice from the stack. At the end of the string we see that we’ve a closing bracket and our stack is empty, so we will add this index to our set.

    We then iterate through our string again and build our return string, skipping over characters which are part of our remove set.
    The solution will work, but we’ve overlooked an edge case when our stack is non-empty, in that case all we’ve to do it do a union of the set and stack indices and keep track of it rather than only the set.

    Here is the solution in python.

    class Solution:
    def minRemoveToMakeValid(self, s: str) -> str:
        stack = []
        remove_set = set()
        for i,char in enumerate(s):
            if char not in "()":
                continue
            elif char == "(":
                stack.append(i)
            elif not stack:
                remove_set.add(i)
            else:
                stack.pop()

        indices_remove = remove_set.union(set(stack))
        output = []
        for i,char in enumerate(s):
            if i in indices_remove:
                continue
            else:
                output.append(char)
        return "".join(output)

    The time complexity will be O(N) as we are doing a two pass solution and the space complexity is O(N) as in the worst case we might have the entire string as invalid.

    Let me know in the comments if you want me to cover other leetcode problems. Thanks for reading.

  • LeetCode 3371 – Identify The Largest Outlier In An Array (Python)

    The problem seems to be pretty popular with Amazon and Meta (formerly known as Facebook) in the past 3 months.

    At its core it’s a math problem and not a programming problem, so if you can figure out the mathematical trick, then this problem is pretty simple.

    We’ve been given an array where n-2 are special numbers and one of the two remaining numbers is the sum of the these special numbers and the other is the outlier. So how do you figure out the outlier?

    The trick is that if you remove the outlier then the array is simply 2S, where S = x_{1}+x_{2}+...+x_{n-2}. So if we take the total sum of the array minus the outlier then it has to be an even number and thus has to be divisible by 2.
    Another thing is that, since the sum of array minus the outlier is 2S, then there must exist a number S in the array. We can check this using a dictionary.

    Our algorithm will be to initialise an outlier variable and then check each number one by one, compute the total minus the number. Check if the total is divisible by 2 and if the half of this number exists in the array, aka, is there a count > 0 in our array. To check this in O(1) time, we maintain a counter of all the numbers in our array. If these conditions are satisfied, then this number could be a possible outlier and we update our outlier variable. If not, we reset the count of the number and our total.

    In the end we will return this outlier.

    from collections import Counter
class Solution:
    def getLargestOutlier(self, nums: List[int]) -> int:
        total_sum = sum(nums)
        counts = Counter(nums)
        outlier = float("-inf")

        for num in nums:
            counts[num]-=1
            total_sum-=num
            if total_sum%2==0 and counts[total_sum//2]>0:
                outlier = max(outlier,num)

            counts[num]+=1
            total_sum+=num
        return outlier

  • LeetCode 1650 – Lowest Common Ancestor of a Binary Tree III

    This question has been asked a lot by Meta (formerly known as Facebook) in the past 3 months.

    The question is categorised as a medium, but if you look at the class structure of the tree, you’ll realise that the answer is pretty straightforward. You could find the LCA by using previous approaches like searching through the entire tree and then getting the LCA, but here we’ve access to the parent node as well in the Node class. Also both, p and q exist in the tree.

    class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

    So all we’ve to do is to build a path set from either p or q to the root. Once this set is built, we then travel from the other node to the root of the binary tree. Once we find the node in the path set, that’s the LCA.

    In this example, our path set from p to root will be {5,3}. We then start at q and iterate towards the root, carefully examining each node along the way. We first check if 4 is in the path; if it is not found, then we move up to 2, and check again. We then move up to its parent 5. Here we find 5 in the path, so we return 5.

    class Solution:
    def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
        path = set()
        while p:
            path.add(p)
            p = p.parent

        while True:
            if q in path:
                return q
            else:
                q = q.parent

    Here we built a path set from p to root. Then we initialise another while loop, and it’s set to run indefinitely as we know LCA will exist as both p and q are in the tree. At each step we take towards the root, we check if q exists in the path set, the moment we find it, that’s the LCA.

    Hope this was helpful and let me know in the comments if you want me to cover other LeetCode questions or machine learning topics.

  • LeetCode 270 – Closest Binary Search Tree Value

    This question has been asked a lot by meta recently.
    You can solve this question either by using a simple inorder traversal, which will take O(n) time and O(n) space complexity, or you can use the property of binary search and solve this in O(logn) time complexity and O(logn) space complexity due to the nature of the Binary Search Tree that values to the left of the node are always smaller than to the right.

    Let’s take a look at the inorder traversal solution.

    class Solution:
    def closestValue(self, root: Optional[TreeNode], target: float) -> int:
        

        self.closest = float("inf")
        def dfs(node):
            if not node:
                return 

            dfs(node.left)

            if abs(self.closest - target) > abs(node.val - target):
                self.closest = node.val

            if abs(self.closest - target) == abs(node.val - target):
                self.closest = min(node.val, self.closest)

            dfs(node.right)

        dfs(root)
        return self.closest

    Here, we begin by creating a variable called closest. We then perform an inorder traversal of the binary search tree, evaluating whether the value of the current node is the closest to our target value. If we find that it is indeed closer, we update our closest variable accordingly. Additionally, we compare it with our previous estimate of closest. If they are equal, we then set our closest variable to the minimum of the two values, as specified in the problem statement.

    Although this initial approach leads to a solution that is acceptable, it has a time complexity of O(n) and a space complexity of O(n). However, we can enhance our efficiency by halving our search space with each decision. In the worst-case scenario—where the tree is unbalanced from the root to the leaf—this method will still operate at O(n) time complexity. On average, though, we achieve a more efficient solution with a time complexity of O(log N).

    By leveraging the properties of binary search trees, we ensure a more optimized search strategy. This not only improves performance but also ensures that our solution scales better with larger datasets.

    class Solution:
    def closestValue(self, root: Optional[TreeNode], target: float) -> int:
        self.closest = float("inf")
        def dfs(node):
            if not node:
                return

            if abs(self.closest - target) > abs(node.val - target):
                self.closest = node.val

            if abs(self.closest - target) == abs(node.val - target):
                self.closest = min(node.val, self.closest)

            if target < node.val:
                dfs(node.left)
            else:
                dfs(node.right)

        dfs(root)
        return self.closest

    Here, we reinitialize our variable closest. Instead of performing an inorder traversal, we check if the value of the current node is closer to the target. We then determine whether the target value is less than the value of the current node. If it is, we conduct a Depth-First Search (DFS) only on the left side of the tree; otherwise, we proceed with a DFS on the right side.

    This approach effectively halves our search space, allowing us to achieve a time complexity of O(log N).

  • LeetCode 3191. Minimum Operations to Make Binary Array Elements Equal to One I

    This question has not been asked by a lot of organisations, but tests your conceptual thinking and algorithmic knowledge of sliding window algorithm.

    The only hint you need is that to convert the first 0 to 1, you’ll need to flip all 3 numbers. And then you need to check if the next number is zero, if it is then you’ll need to again flip the 3 digits. At the end of this you’ll then check if the sum of the array is equal to its length. If that’s the case, then you’ve your answer. Otherwise you can’t make all elements equal to 1 and you should return -1.

    For example.

    [0,1,1,1,0,0] -> [1,0,0,1,0,0] -> [1,1,1,0,0,0] -> [1,1,1,1,1,1]

    In the above example we needed 3 operations to make the array elements equal to one.

    [0,1,1,1] -> [1,0,0,1] -> [1,1,1,0]

    In this example you can see that we can’t flip the last 0 only, if we do so then the 1s before it will become zero. So if we traverse the list, we can never get all the elements of the array to become 1. In this example we will return -1.

    Below is the solution to the problem.

    class Solution:
    def minOperations(self, nums: List[int]) -> int:
        i = 0
        num_op = 0
        for i in range(2,len(nums)):
            if nums[i-2] == 0:
                num_op+=1
                nums[i-2] = nums[i-2]^1
                nums[i-1] = nums[i-1]^1
                nums[i] = nums[i]^1

        if sum(nums) == len(nums):
            return num_op
        else:
            return -1

    The time complexity is O(n) as we do traverse through the entire array. The space complexity is O(1) as we only store variables like i and num_op which take constant space.

  • LeetCode 2594 – Minimum Time To Repair Cars

    LeetCode 2594 – Minimum Time To Repair Cars

    Although this problem is not frequently asked by companies, it offers an interesting perspective. Initially, this problem may seem to require a complex solution, but it can be efficiently solved using binary search.

    Binary Search Approach

    The key is to frame the problem as finding the minimum time required to repair all cars, within a range from 1 to the maximum possible time. The maximum possible time is determined by the minimum rank multiplied by the square of the number of cars. Since the number of cars is always greater than 0, the theoretical minimum possible time is 1, and the solution lies within this range.

    Therefore, the problem is transformed into a binary search, where at each iteration, we check if all cars can be repaired within a given time. If yes, we search the left half for a potentially lower time; otherwise, we search the right half.

    We know that a mechanic with rank ‘r’ takes r*n^{2} time to repair ‘n’ cars, so within time ‘t’, they can repair​ sqrt(t/r) cars. We need to create a helper function that returns a boolean indicating whether all cars can be repaired within a given time ‘t’. We have to take the floor and then we sum the values to determine number of cars that can be repaired in time t. If this value is greater than or equal to the desired number of cars, we will return True.

    def can_repair(self, t,n,ranks):
        n_each_mech = [int((t/r)**0.5) for r in ranks]
        return sum(n_each_mech)>=n

    The solution to the problem.

    class Solution:
    def repairCars(self, ranks: List[int], cars: int) -> int:
        min_rank = min(ranks)
        low = 1
        high = min_rank*cars*cars

        min_time = None

        while low <= high:
            mid = (high+low)//2

            if self.can_repair(mid,cars,ranks):
                min_time = mid
                high = mid-1

            else:
                low = mid+1
        
        return min_time

    def can_repair(self, t,n,ranks):
        n_each_mech = [int((t/r)**0.5) for r in ranks]
        return sum(n_each_mech)>=n

    Complexity Analysis

    The time complexity is O(N log(C)), where N is the number of mechanics and C is the range of possible times. The binary search contributes a factor of O(log(C)), and the can_repair function contributes a factor of O(N). The space complexity is O(1) as we are only using constant extra space.

    Let me know if you would like to cover any additional aspects or if you have any further questions.

  • LeetCode 2529 – Maximum Count of Positive Integer and Negative Integer

    The question has been asked by a few companies including Meta, but is not a super popular question.

    Nonetheless the question is important as it focusses on a variation of binary search.

    The naive solution to the problem would be iterating through the array, finding out the first index you see a positive number, also keeping track the last index you saw a negative number. Then you can then calculate the number of positive numbers and number of negative numbers in the list. But this would be O(n) in time complexity. We can solve this problem by using binary search and this will bring down the time complexity to O(logn).

    The trick is to phrase the question as to finding the index of the first occurrence of positive number. Since the array is sorted, we can then calculate the number of positive integers.

    We also need to find the last occurence of a negative number in the array. This will then provide us the information about how many negative numbers are there in the array.

    Also remember that the array is not guaranteed to have both positive or negative integers, so we need to take that into account as well.

            n = len(nums)

        # First positive index
        l,r = 0,n-1
        first_positive_idx = n
        while l <= r:
            mid = (l+r)//2
            val = nums[mid]
            if val > 0:
                first_positive_idx = mid
                r = mid-1
            else:
                l = mid+1

    Here we initialise the first positive index to be n as it may be the case that the array either has all 0s or negative integers, in that case the first positive index has to be outside our array and the first place it can go into is n. We calculate the number of positive integers as n – first_positive_idx, so if it’s at n then we know there are 0 positive integers in the array.

    The binary search is the standard binary search, except we search if the value in the middle is positive, if that’s the case we mark that as a possible first positive index and then search towards the left as there could be more positive in the left, otherwise we search in the right half. 

            # Last negative index
        l,r = 0,n-1
        last_neg_idx = -1
        while l <= r:
            mid = (l+r)//2
            val = nums[mid]
            if val < 0:
                last_neg_idx = mid
                l = mid + 1
            else:
                r = mid-1

    Similarly for the last negative index, we initialise the last negative index to be -1, which is that if all integers in the array are 0 or positive, then its position has to be outside the array. We calculate the number of negative integers as last_negative_idx + 1, so here it will automatically become 0.

    We then do a binary search where we check if the middle element is negative, if we find it then we mark it as a possible last negative index and then search towards the right as there could be more negative numbers, otherwise we search in the left half.

    Combining everything we have the solution.

    class Solution:
    def maximumCount(self, nums: List[int]) -> int:

        
        
        n = len(nums)

        # First positive index
        l,r = 0,n-1
        first_positive_idx = n
        while l <= r:
            mid = (l+r)//2
            val = nums[mid]
            if val > 0:
                first_positive_idx = mid
                r = mid-1
            else:
                l = mid+1
        # Last negative index
        l,r = 0,n-1
        last_neg_idx = -1
        while l <= r:
            mid = (l+r)//2
            val = nums[mid]
            if val < 0:
                last_neg_idx = mid
                l = mid + 1
            else:
                r = mid-1

        num_positive = n-(first_positive_idx)
        num_negative = (last_neg_idx) + 1

        return max(num_positive,num_negative)

    As you can see the time complexity is O(logn) as we do two binary searches. There is a way to combine both in one pass but in terms of time complexity, it doesn’t matter. It has a space complexity of O(1) as we are not storing anything other than some variables which take up constant space.

    Thanks for reading the article, let me know in the comments which problems you want me to either write the solution or create a youtube walkthrough in the comments.

  • LeetCode 346. Moving Average from Data Stream (Python)

    This is a premium problem on LeetCode and has also been asked by Meta as of the date of publishing almost 50 times.

    The problem statement is pretty simple, given an incoming integer stream, you have to calculate the simple moving average. The size or the window is also given. 

    class MovingAverage:

    def __init__(self, size: int):
        

    def next(self, val: int) -> float:
        


# Your MovingAverage object will be instantiated and called as such:
# obj = MovingAverage(size)
# param_1 = obj.next(val)

    Now a naive solution would be to initialise a data structure like an array and keep appending elements which are given in the next method and then compute the average of the last n elements, n being the size, every time. 

    from statistics import mean
class MovingAverage:

    def __init__(self, size: int):
        self.size = size
        self.nums = []

    def next(self, val: int) -> float:
        self.nums.append(val)
        return mean(self.nums[-self.size:len(self.nums)])

    Now this will work, but there are two issues here. One we’re storing elements not required, meaning we only need to store the latest numbers till the dimension of size. Also, there is a lot of repeated work here, where we’re calculating the mean every time. Making this solution O(N) in time complexity and also O(N) in space complexity.

    We can improve on both aspects. First, we will use a queue to store our numbers. The reason for doing so is that once the size of the queue becomes equal to our window size. We will pop elements from the left and add the numbers on the right. To do this efficiently, we will use the deque data structure in python.
    We will also create a variable called sum, where we will track the running sum. This will allow us to compute the moving average in O(1) time complexity.

    from collections import deque
class MovingAverage:

    def __init__(self, size: int):
        self.size = size
        self.sum = 0
        self.vals = deque()

    def next(self, val: int) -> float:
        if len(self.vals) >= self.size:
            self.sum -= self.vals.popleft()
        self.sum+=val
        self.vals.append(val)
        return self.sum/len(self.vals)

    Here, you can see that we keep track of what the size of our self.vals is. If it exceeds the window size, we pop from the left and decrease our running sum.
    No matter what the size is, we always increment our sum and also append the number to our queue.

    There might be some minor improvements, but in terms of time and space complexity, this is the most optimal solution.

    Let me know if you found this solution helpful. I’ll be posting more LeetCode solutions on the blog as I feel they are also an integral component to cracking Machine Learning jobs, especially at Meta, Google etc.

  • 10 Decision Tree Questions Every Data Scientist Needs to Know

    You may or may not be asked such questions in an interview, but often these kind of questions come up in screening tests which have MCQs.