Tag: F1score

Macro vs micro averages, how are they calculated ?
In this post, I’ll go over macro and micro averages, namely precision, and recall.

What is macro and micro averages ?

A macro takes the measurement independently of each class and then takes the average, thus giving equal weight to each class whereas a micro will take the class imbalances into account when computing the average.

When to use macro vs micro averages ?

If you suspect class imbalances to be there, then micro average should be preferred to macro.

How are they different ?

Let’s take an example scenario from here.
```
from sklearn.metrics import precision_score
y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
precision_score(y_true, y_pred, average='macro')
0.22...
precision_score(y_true, y_pred, average='micro')
0.33...
```
You can see that the precision score is different for macro calculation vs micro calculation.

Breaking down the calculation here in the confusion matrix

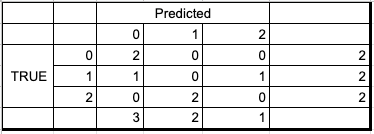
A quick recap the the precision formula is for binary classification problem –

$Precision = \frac{TP}{TP+FP}$

For multi-class the micro and macro formula can be written as – $Precision_{micro} = \frac{\sum TP_{i} }{\sum TP_{i}+\sum FP_{i}}$

$Precision_{macro} = \frac{\sum PR_{i} }{n}$

So in the above example, the micro precision is
Similarly the Precision for each class individually is

P(0) = 2/3 = 0.66, P(1) = 0, P(2) = 0

So macro precision is
In this way the micro vs macro averages differ. Hope this article cleared your problems on macro vs micro averages in ML metrics.
January 11, 2023
When to use F2 or F0.5 score ? (F-beta score)
Whenever we come across an imbalanced class problem, the metric to measure is often F1 score and not accuracy. A quick reminder that the F1 score is the harmonic mean of precision and recall.
Precision is how accurate is your ML model in its predictions.
Recall is a measure of the model’s ability to correctly identify the positive class.
So the F1 score is a balanced measure of both recall and precision. But what if you want to prioritize reducing false positives or reducing false negatives, there comes F-beta. It’s a generalized metric, where a parameter beta is introduced to generalize the F-score.
This enables one to choose an appropriate beta value to tune for the task at hand. If you want to minimize false positives, you want to increase the weight of precisions, so you should choose a value of beta less than 1, typically 0.5 is chosen and is called F0.5 score.

Similarly, if you want to increase the importance of recall and reduce false negatives, you should choose a value of beta greater than 1, typically 2 is selected and is called F2 score.

In a nutshell, you should optimize F2 score to reduce false negatives and F0.5 score to reduce false positives.
January 9, 2023