Tag: Gradient Descent

An Illustrated Guide to Gradient Descent
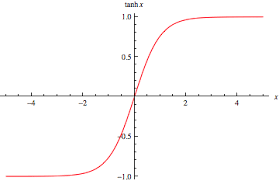
How will you minimise this function –

$f(x) = x^{2}$

The mathematical solution will be to find the derivative, then solve the equation, $\frac{\partial f(x)}{\partial x} = 2x = 0$ , which gives the solution as x = 0. But what if you don’t know this and need to rely on a method which can reach the minimum of a function iteratively. That is what gradient descent does.

Gradient descent as the name suggests is like slowly descending down the mountain that is the loss function but in an iterative manner. We always take a small step in the opposite direction of the gradient. If the gradient is positive, we take a negative step and if the gradient is negative then we take a positive step.

So in this example suppose we have to minimise $x^{2}$ and we start off with an initial value say 7. Then we we will update the value of x as –

x_new = x_old + (- $\frac{\partial f(x)}{\partial x}$ )*x_old*lr

where lr is the learning rate. Tuning this value is crucial is how fast we reach the minimum, or if we overshoot the minimum and never reach it.

Let’s take an example in python –
```
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np

def f(x):
    return x**2

def derivative(x):
    return 2*x

y = [f(x) for x in np.arange(-20,20,0.2)]
x = np.arange(-20,20,0.2)

plt.plot(x,y)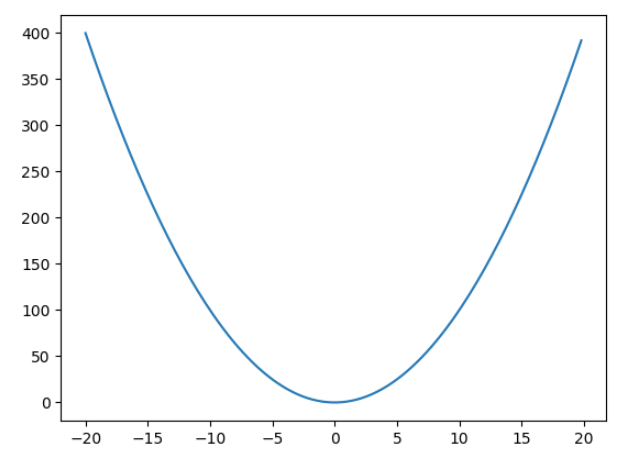
```
```
value = 7
lr = 0.1
derivatives = []
values = []
for i in range(9):
    values.append(value)
    derivatives.append(derivative(value))
    value = value - lr*derivative(value)

# List of points and derivatives
points = [(x,f(x)) for x in values]

# Create a 9x9 subplot grid
fig, axs = plt.subplots(3, 3, figsize=(9, 9))


# Plot the main plot (x^2) in the top-left subplot
axs[0, 0].plot(x, y, label='$x^2$', color='blue')
axs[0, 0].legend()

# Iterate over points and derivatives to create subplots
for i, (point_x, point_y) in enumerate(points):
    # Calculate the line passing through the point with the slope from the derivatives list
    slope = derivatives[i]
    line_y = x + slope * (x - point_x)

    axs[i//3, i%3].plot(x, y, color='blue')

    # Plot the point
    axs[i//3, i%3].plot(point_x, point_y, marker='x', markersize=10, color='red', label='Point')
    
    # Plot the line passing through the point with the specified slope
    axs[i//3, i%3].plot(x, line_y, linestyle='--', color='green', label=f'Slope = {slope}')

    # Set titles for subplots
    axs[i//3, i%3].set_title(f'Point at ({np.round(point_x,2)}, {np.round(point_y,2)})')

# Adjust layout for better visualization
plt.tight_layout()

# Show the plot
plt.show()
```
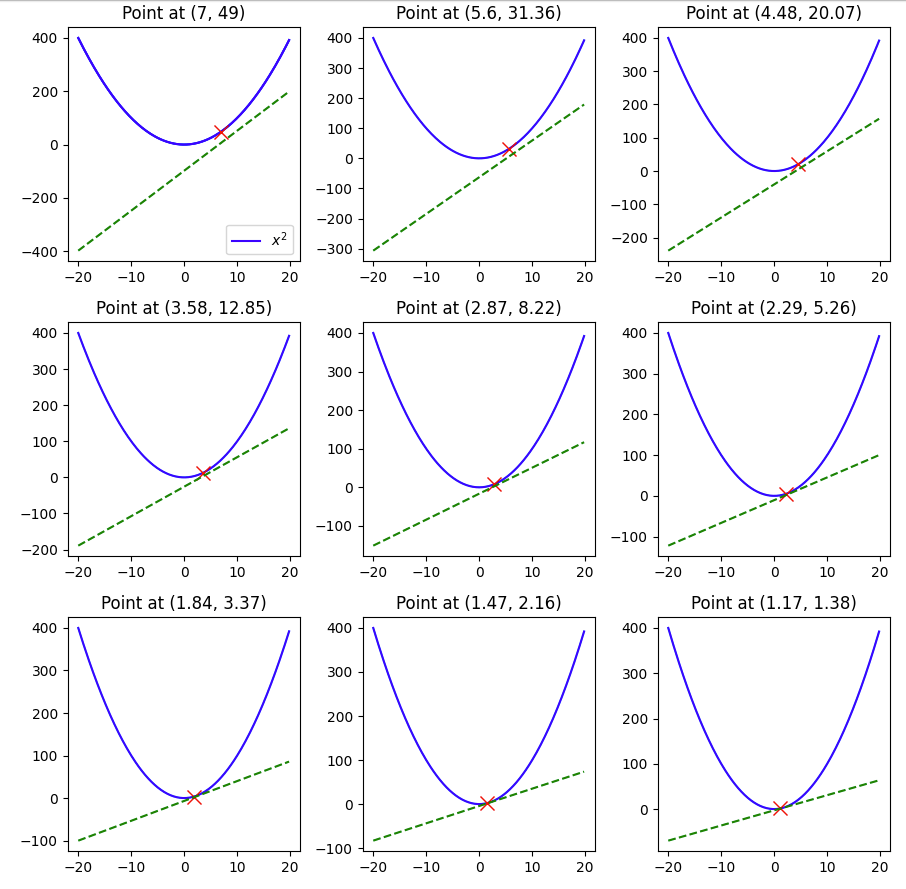
Here we see that with a learning rate of 0.1 and a starting value of 7 and in 9 steps we were able to reach 1.17, pretty close to the minimum of 0, but not quite so, if we change the lr to 0.3, let’s see what happens.

The minimum of 0 was reached within 9 steps.

But what happens if we make the lr 1 –

Here you can see that the value keeps oscillating between 7 and -7, and thus having a large learning rate also can be harmful when using ML models that use gradient descent.

Hopefully this example gave you a visual guide on how gradient descent works.
January 22, 2024
Why Tanh is a better activation function than sigmoid ?
You might be asked that why often in neural networks, tanh is considered to be a better activation function than sigmoid.

Sigmoid

Tanh

Andrew NG also mentions in his deep learning specialization course that tanh is almost always a better activation function than sigmoid. So why is that the case?

There are a few reasons why the hyperbolic tangent (tanh) function is often considered to be a better activation function than the sigmoid function:
1. The output of the tanh function is centered around zero, which means that the negative inputs will be mapped to negative values and the positive inputs will be mapped to positive values. This makes the learning process of the network more stable.
2. The tanh function has a derivative that is well-behaved, meaning that it is relatively easy to compute and the gradient is relatively stable.
3. The sigmoid function, on the other hand, maps all inputs to values between 0 and 1. This can cause the network to become saturated, and the gradients can become very small, making the network difficult to train.
4. Another reason is that the range of the tanh function is [-1,1], while the range of the sigmoid function is [0,1], which makes the model output values more similar to the standard normal distribution. It will be less likely to saturate and more likely to have a good gradient flow, leading to faster convergence.
5. Another advantage is that the tanh function is differentiable at all points. In contrast, the sigmoid function has a kink at 0, which may cause issues when computing gradients during back-propagation, and other optimization methods.
All that being said, whether to use sigmoid or tanh depends on the specific problem and context, and it’s not always the case that one is clearly better than the other.
January 11, 2023