Tag: Python

Time Series Forecasting with Python Part 3 – Identifying Trends in Data
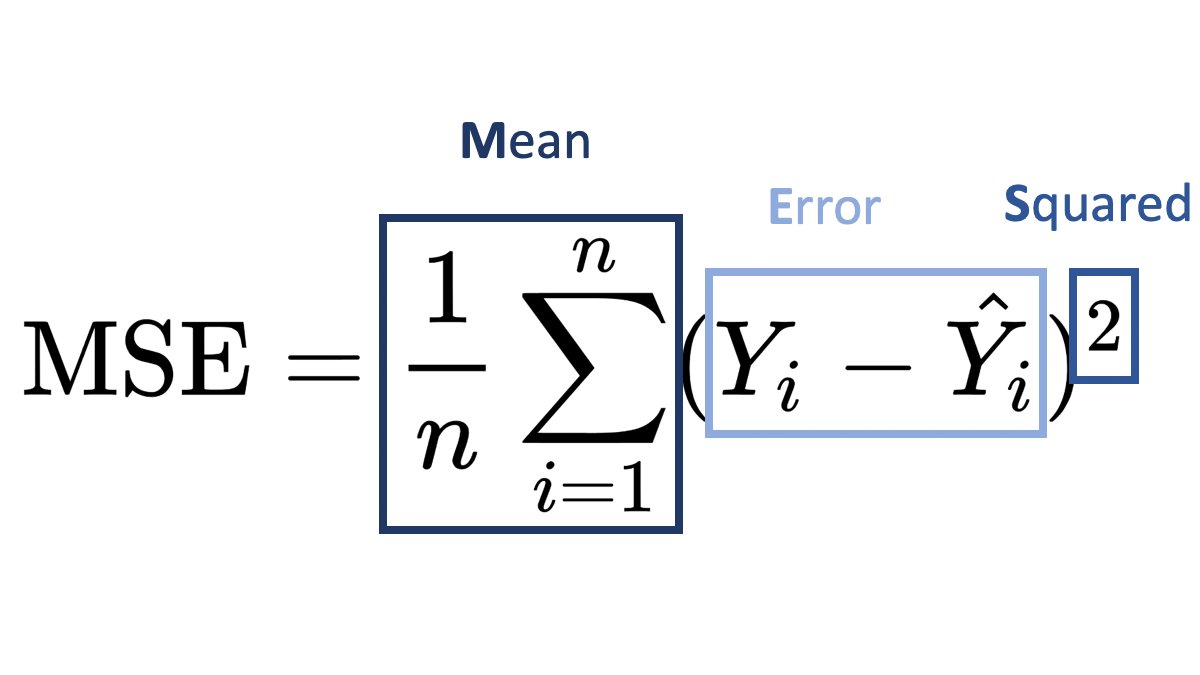
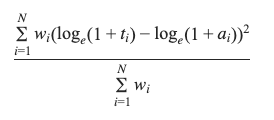While doing time series forecasting it is very important to analyse if your data has some trends, seasonality or periodicity in it. To identify if a time series has seasonality there are several techniques you can use.

We will be using the following dummy data to see how we can test for seasonal trends in our data.
```
sales = np.array([100, 120, 130, 150, 110, 130, 140, 160, 120, 140, 150, 170])

quarters = ['Q1 2018', 'Q2 2018', 'Q3 2018', 'Q4 2018',
            'Q1 2019', 'Q2 2019', 'Q3 2019', 'Q4 2019',
            'Q1 2020', 'Q2 2020', 'Q3 2020', 'Q4 2020']
```
1. Visual inspection – Just by looking at the plot of the time series, you can identify that there are visible patterns in it.
In the image above you can clearly see that the sales grow from Q1 to Q3 and then decline in Q4 year on year.

2. Autocorrelation Function (ACF) – Autocorrelation refers to the correlation of a series with itself at different time lags. In other words, it quantifies the similarity or relationship between a data point and its preceding or lagged observations. The ACF helps identify any repeating patterns or dependencies within the time series data.

In the ACF plot, if we see spikes at regular lag intervals, it indicates seasonality. We can take the help of plot_acf from the statsmodels package.
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf

# Generate ACF plot
fig, ax = plt.subplots(figsize=(10, 6))
plot_acf(sales, lags=11, ax=ax)  # Set lags to the number of quarters (12) minus 1

plt.title('Autocorrelation Function (ACF) Plot')
plt.xlabel('Lag')
plt.ylabel('Autocorrelation')
plt.show()
```
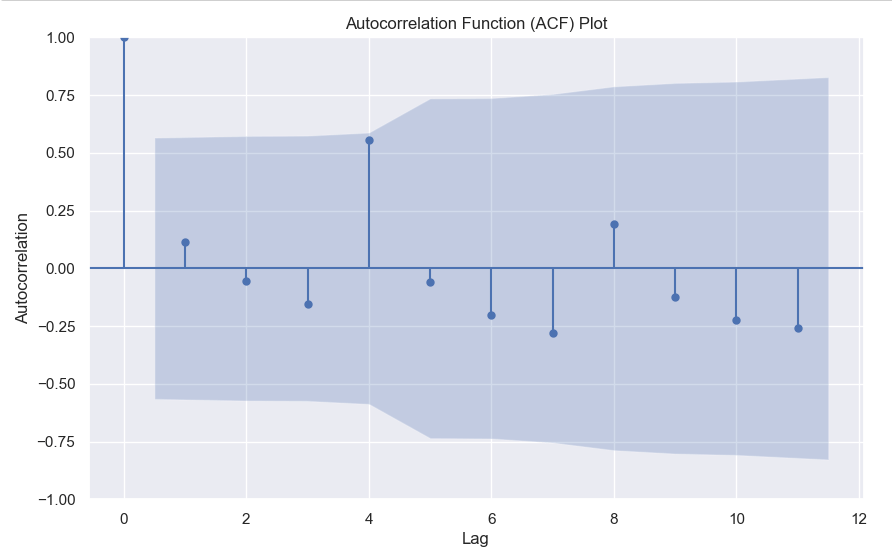
Here we can clearly see a spike at 4, indicating what we already know that there is a seasonality present within the time series data.

3. Decomposition –

Decomposition is a technique used to break down a time series into its individual components: trend, seasonality, and residual (also known as error or noise). The decomposition process allows us to isolate and analyze these components separately, providing insights into the underlying patterns and variations within the time series data.

There are two commonly used types of decomposition:
1. Additive
2. Multiplicative.
1. Additive Decomposition: In additive decomposition, the time series is assumed to be the sum of its components. It is expressed as:Y(t) = Trend(t) + Seasonality(t) + Residual(t)
  The additive decomposition assumes that the magnitude of the seasonal fluctuations remains constant throughout the time series.
2. Multiplicative Decomposition: In multiplicative decomposition, the time series is assumed to be the product of its components. It is expressed as:Y(t) = Trend(t) * Seasonality(t) * Residual(t)
  Multiplicative decomposition assumes that the seasonal fluctuations grow or shrink proportionally with the trend.
Again we will be using the statsmodels package to perform seasonal decomposition.
```
from statsmodels.tsa.seasonal import seasonal_decompose

# Create a pandas Series with a quarterly frequency
index = pd.date_range(start='2018-01-01', periods=len(sales), freq='Q')
series = pd.Series(sales, index=index)

# Perform seasonal decomposition
decomposition = seasonal_decompose(series, model='additive')

# Extract the components
trend = decomposition.trend
seasonality = decomposition.seasonal
residuals = decomposition.resid

# Plot the components
plt.figure(figsize=(10, 8))
plt.subplot(411)
plt.plot(series, label='Original')
plt.legend(loc='best')
plt.subplot(412)
plt.plot(trend, label='Trend')
plt.legend(loc='best')
plt.subplot(413)
plt.plot(seasonality, label='Seasonality')
plt.legend(loc='best')
plt.subplot(414)
plt.plot(residuals, label='Residuals')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
```
In this dummy example, we can clearly see via this decomposition that there is an upwards trend in the data along with a quarterly seasonality.

There are a couple more tests left to explore, but we will pick those up in the next part where we will continue to explore this seasonality and trends in time series data.
June 28, 2023
Store Metadata within your model – Catboost
Often after training a ML model, you want to move it to production, sometimes you also want to store certain metadata about the model like its author, version, or other characteristics about it.

The first solution that comes to mind is creating a JSON or Python file within your repository and storing those there, but you can actually store metadata within the model file. I’ll show two examples of how you can do so in xgboost and catboost.

For catboost the code snippet is below, it is pretty straightforward.
```
from catboost import CatBoostRegressor

# Define your metadata
metadata = {
    'author': 'John Doe',
    'description': 'CatBoost model for classification',
    'version': '1.0',
    # Add any other metadata fields as needed
}

# Initialise your model with the added metadata
model = CatBoostRegressor(metadata=metadata)
# Fit the model on your data
model.fit(X,y)

model.save_model('/path/to/model.cbm')
```
Then you can load the model back using the below snippet and inspect the metadata stored within your model file.
```
model = CatBoostRegressor()
model.load_model('/path/to/model.cbm')

print(model.get_metadata()['author'])
>>> John Doe
```
For Xgboost, you can visit this link.
June 27, 2023
10 Decision Tree Questions Every Data Scientist Needs to Know

You may or may not be asked such questions in an interview, but often these kind of questions come up in screening tests which have MCQs.

June 27, 2023

Using Custom Eval Metric with Catboost

Catboost offers a multitude of evaluation metrics. You can read all about them here, but often you want to use a custom evaluation metric.

For example in this ongoing Kaggle competition, the evaluation metric is Balanced Log Loss. Such a metric is not supported by catboost. By this I mean that you can’t simply write this and expect it to work.

from catboost import CatBoostClassifier
model = CatBoostClassifier(eval_metric="BalancedLogLoss")
model.fit(X,y)

This will give you an error. What you need to define is a custom eval metric class. The template for which is pretty simple.

class UserDefinedMetric(object):
    def is_max_optimal(self):
        # Returns whether great values of metric are better
        pass

    def evaluate(self, approxes, target, weight):
        # approxes is a list of indexed containers
        # (containers with only __len__ and __getitem__ defined),
        # one container per approx dimension.
        # Each container contains floats.
        # weight is a one dimensional indexed container.
        # target is a one dimensional indexed container.

        # weight parameter can be None.
        # Returns pair (error, weights sum)
        pass

    def get_final_error(self, error, weight):
        # Returns final value of metric based on error and weight
        pass

Here there are three parts to the class.

get_final_error – Here you can just return the error, or if you want to modify the error like take the log or square root, you can do so.
is_max_optimal – Here you return True if greater is better like accuracy etc, otherwise return False.
evaluate – Here lies the meat of your code where you’ll actually write what metric you want. Remember that the approxes are the predictions and you need to take approxes[0] as the output.

Below you will find the code for Balanced Log Loss as an eval metric.


class BalancedLogLoss:
    def get_final_error(self, error, weight):
        return error

    def is_max_optimal(self):
        return False

    def evaluate(self, approxes, target, weight):
        y_true = target.astype(int)
        y_pred = approxes[0].astype(float)
        
        y_pred = np.clip(y_pred, 1e-15, 1 - 1e-15)
        individual_loss = -(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
        
        class_weights = np.where(y_true == 1, np.sum(y_true == 0) / np.sum(y_true == 1), np.sum(y_true == 1) / np.sum(y_true == 0))
        weighted_loss = individual_loss * class_weights
        
        balanced_logloss = np.mean(weighted_loss)
        
        return balanced_logloss, 0.0

Then you can simply call this in your grid search or randomised search like this –model = CatBoostClassifier(verbose = False,eval_metric=BalancedLogLoss())

Write in the comments below if you’ve any questions related to custom eval metrics in Catboost or any ML framework.

June 24, 2023

Cohen’s D – How to measure the difference in distributions
While the t-test or Mann-Whitney U test can tell you whether two distributions are different from each other, it doesn’t tell you the degree to which they are different.

For this purpose, you can calculate Cohen’s D.

$Cohens'D = \frac{(M1-M2)}{S_{pooled}}$

Where the pooled standard deviation can be defined as

$S_{pooled} = \sqrt{\frac{s_{1}^{2} + s_{1}^{2}}{2}}$

After calculating Cohen’s D you can gauge the difference via this thumb rule –
- Small effect = 0.2
- Medium Effect = 0.5
- Large Effect = 0.8
Below you can find the code to calculate Cohen’s D in python
```
import numpy as np

def cohens_d(x,y):
    var_x = np.var(x)
    var_y = np.var(y)
    mean_x = np.mean(x)
    mean_y = np.mean(y)
    pool_variance = np.sqrt((var_x**2 + var_y**2)/2)
    return (mean_x - mean_y)/pool_variance
```
Write in the comments in case you’ve any questions regarding cohen’s D.
June 17, 2023
MSE vs MSLE, When to use what metric?
MSLE (Mean Squared Logarithmic Error) and MSE (Mean Squared Error) are both loss functions that you can use in regression problems. But when should you use what metric?

Mean Squared Error (MSE):

It is useful when your target has a normal or normal-like distribution, as it is sensitive to outliers.

An example is below –

In this case using MSE as your loss function makes much more sense than MSLE.

Mean Squared Logarithmic Error (MSLE):
- MSLE measures the average squared logarithmic difference between the predicted and actual values.
- MSLE treats smaller errors as less significant than larger ones due to the logarithmic transformation.
- It is less sensitive to outliers than MSE since the logarithmic transformation compresses the error values.
An example where you can use MSLE –

Here if you use MSE then due to the exponential nature of the target, it will be sensitive to outliers and MSLE is a better metric, remember that MSLE cannot be used for optimisation, it is only an evaluation metric.

In general, the choice between MSLE and MSE depends on the nature of the problem, the distribution of errors, and the desired behavior of the model. It’s often a good idea to experiment with both and evaluate their performance using appropriate evaluation metrics before finalizing the choice.
May 31, 2023
Numpy Argpartition – How it works?
We all know that to find the maximum value index we can use argmax, but what if you want to find the top 3 or top 5 values. Then you can use argpartition.

Let’s take an example array.
```
x = [10,1,6,8,2,12,20,15,56,23]
```
In this array, it’s very easy to find the maximum value index, it’s 8.

But what if you want the top 3 or top 5, then you can use np.argmax.

How it works is that it first sorts the array and then partitions the array on the kth element. All elements lower than the kth element will be behind it and larger ones will be after it.

Let’s see with a few examples.
```
idx = np.argpartition(x, kth=-3)
print(idx)
>>> [1 4 2 3 0 5 7 6 8 9]
print([x[i] for i in idx ])
>>> [1, 2, 6, 8, 10, 12, 15, 20, 56, 23]
```
Here you can see that you get the top 3 indices as the last 3 values of the list, you can simply filter the values you can want by using idx[-3:].

Similarly for the top 5 –
```
idx = np.argpartition(x, kth=-5)
print(idx[-5:])
>>> [5 7 6 8 9]
```
Hopefully, this post explains how you can use arg-partition to get the top k element indices. If you have any questions, feel free to ask in the comments or here on my Youtube Channel.
April 22, 2023
MCC Score – The only ML metric you need

The title might be a bit of a clickbait, but MCC (Matthews Correlation Coefficient) is a critical ML metric that every Data Scientist must know.

Metrics like the F1 score focus on only one class and its performance, but if you want a balanced model then you should be optimising your model on MCC score rather than on Accuracy or F1-score.

Let us take an example of –

y_true = [1,1,1,1,0,0,1, 0,1] y_pred = [1,1,1,1,1,1,1, 0,0]

If we calculate the F1-score then it is ~0.77, but the MCC score is ~0.19, meaning that even though the model is very good at classifying the positive class, it is not very good at the negative class.

If we look at the formula for MCC –
\[MCC = \frac{(TPxTN)-(FPxFN)}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}\] https://www.hostmath.com/Math/MathJax.js?config=OK
It should be clear that MCC gives equal focus on both TP and TN, since it is a correlation coefficient, its value ranges from -1 to 1.

February 5, 2023
ML Metrics | Top N Accuracy Explained
This metric is usually used in multiclass classification problems.
Each multiclass model gives a probability score for all the classes it is being trained on, but often you take the highest one, by using np.argmax but what if you took the top n classes and gave credit to the model if it got right in one of the n predictions.
That is what is top n accuracy, it gives the model more chances to be right.

Lets take an example.

Suppose you built a model that predicts 3 classes and you want to find the top 2 accuracy of your model.
Then you would pass the prediction array to the model and the true values and if the correct prediction is in the top 2 then you give it credit for being right.
```
import numpy as np
from sklearn.metrics import top_k_accuracy_score
y_true = [0,1,1,2,2]
y_pred = [[0.25, 0.2,0.3], #Here 0 is in the top 2
          [0.3, 0.35, 0.5], #Here 1 is in the top 2
          [0.2,0.4, 0.45], #Here 1 is in the top 2
          [0.5, 0.1, 0.2], #Here 2 is in the top 2
          [0.1, 0.4, 0.2]] #Here 2 is in the top 2
top_k_accuracy_score(y_true, y_pred, k=2)
```
It is 1.0, because the correct class was always in our top 2 prediction, actually, if you notice then it was always the second prediction of our model, so if we take regular accuracy or set the value k = 1 in top_k_accuracy_score(y_true, y_pred, k=2), the answer is 0.

Hopefully, this explains what top N accuracy is, and if you want me to cover any ML topic, write in the comments below. Thanks for reading.
January 27, 2023
5 Essential Boosting Parameters You Should Be Tuning
Here are the 5 essential hyper-parameters that you should be always tuning when building any boosting model, whether you’re using XgBoost, LightGBM or even CatBoost.
1. n_estimators – It is not the number of trees that the boosting algorithm will grow, but as the name suggests, the number of times gradient boosting will occur, so if you are using a tree-based boosting algorithm, then if you make this number 5, then each round of boosting fits a single tree to the negative gradient of some loss function.
2. max_depth – The depth of each tree, pretty simple, the higher this number, the stronger each learner is in the model and the more your model can overfit. So pretty important to tune.
3. learning_rate – Again a very important param, the higher it is the faster your algorithm will converge to the local minima, but too high and it might overshoot the minima, too low and it might never reach the minima.
4. subsample – Sample of the training data to be used in each boosting round, if you use 0.5, then xgboost will randomly sample half your training data in each boosting iteration before growing the tree. Important if you want to control overfitting.
5. colsample_bytree – Fraction of columns to use when growing a tree, again if set to 0.5, xgboost will randomly sample half of your features to grow the tree in each boosting round. Again very important to control overfitting.
In another post I’ll be going over another 5 essential hyper-parameters that you should be tuning.
January 26, 2023