ML EXPLAINED

Tag: Regression

  • Creating a Custom Loss Function For Machine Learning Models

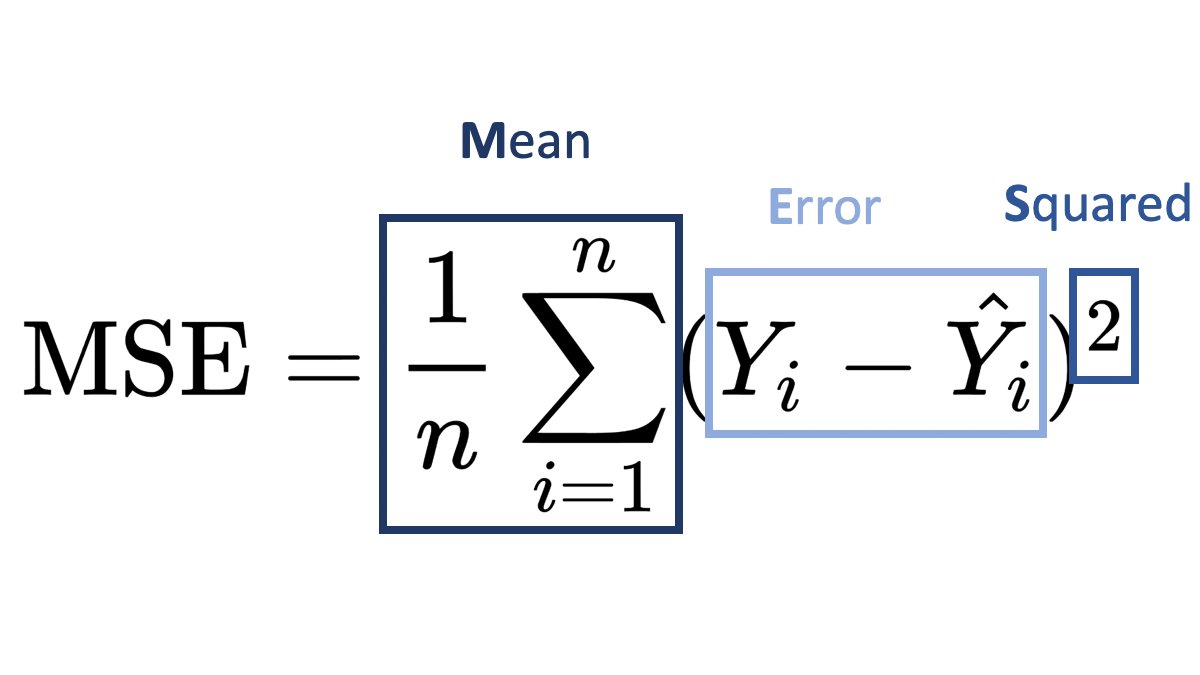
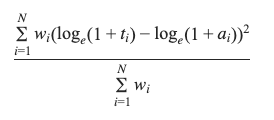    While standard Machine Learning Libraries provide a vast array of loss functions out of the box, sometimes we need to create our own custom loss function. In this blog post, I’ll go over a simple example and create a custom loss function in Catboost.

    First we will create the data for training.

    # Importing libraries
    import numpy as np
    import pandas as pd
    from sklearn.metrics import mean_squared_error
    from catboost import CatBoostRegressor, Pool
    from sklearn.datasets import fetch_california_housing

    raw_data = fetch_california_housing()

    data = pd.concat([pd.DataFrame(raw_data['data'], columns=raw_data['feature_names']), 
                      pd.Series(raw_data['target'], name = 'target')], axis = 1)

    features = [i for i in data.columns.tolist() if i != 'target']

    Since the objective is not to create the best model possible, we won’t be doing any feature engineering. Let’s use catboost, and create a model using standard loss functions. 

    model = CatBoostRegressor(loss_function='RMSE', n_estimators=100, eval_metric='RMSE')

    cb_pool = Pool(data=data[features], label=data['target'], feature_names=features)

    model.fit(cb_pool)

    predictions = model.predict(cb_pool)

    mean_squared_error(y_true=data['target'], y_pred=predictions)

    Upon evaluating the model we find that the mean squared error is 0.15. Definitely a model which is overfitting, but that’s not a concern for this tutorial.

    But what is you don’t want to use RMSE as a loss function, and instead want to use something like this –

    loss = \frac{\sum (y - \hat{y})^{4}}{n}

    Then how do you create a loss function in catboost?

    For this, you’ll need to calculate the first derivative and the second derivative of the loss function with respect to \hat{y}.

    Using the chain rule, the first derivative is

    \frac{\partial (y-\hat{y})^4}{\partial \hat{y}} = \frac{\partial (y-\hat{y})^4}{\partial (y-\hat{y})}*\frac{\partial y - \hat{y}}{\partial \hat{y}} = 4 * (y - \hat{y})^{3}* -1 = -4(y -\hat{y})^{3}

    And similarly using the chain rule, the second derivative comes out to be 12*(y-\hat{y})^2

    The catboost template for a custom objective is as follows – 

    class UserDefinedObjective(object):
    def calc_ders_range(self, approxes, targets, weights):
        """
        Computes first and second derivative of the loss function 
        with respect to the predicted value for each object.

        Parameters
        ----------
        approxes : indexed container of floats
            Current predictions for each object.

        targets : indexed container of floats
            Target values you provided with the dataset.

        weight : float, optional (default=None)
            Instance weight.

        Returns
        -------
            der1 : list-like object of float
            der2 : list-like object of float

        """
        pass

    Using this temple, we can write the custom objective –

    class CustomLossObjective(object):
        def calc_ders_range(self, approxes, targets, weights):
            assert len(approxes) == len(targets)
            if weights is not None:
                assert len(weights) == len(approxes)
            
            result = []
            n = len(targets)  # Number of samples

            for index in range(len(targets)):
                error = targets[index] - approxes[index]
                der1 = -4 * error**3
                der2 = 12 * error**2

                if weights is not None:
                    der1 *= weights[index]
                    der2 *= weights[index]

                result.append((der1, der2))
            return result

    Now let’s use this custom loss in our model

    model = CatBoostRegressor(loss_function=CustomLossObjective(), n_estimators=100, eval_metric='RMSE')
    model.fit(cb_pool)

    predictions = model.predict(cb_pool)
    mean_squared_error(y_true=data['target'], y_pred=predictions)

    Using this loss, we see that the mean squared error is 0.735, this is clearly inferior to using RMSE, but as mentioned before the objective of this blog post is not to build the best model but to showcase how one can create a custom loss objective in catboost.

  • MSE vs MSLE, When to use what metric?

    MSLE (Mean Squared Logarithmic Error) and MSE (Mean Squared Error) are both loss functions that you can use in regression problems. But when should you use what metric?

    Mean Squared Error (MSE):

    It is useful when your target has a normal or normal-like distribution, as it is sensitive to outliers.

    An example is below –

    In this case using MSE as your loss function makes much more sense than MSLE.

    Mean Squared Logarithmic Error (MSLE):

    • MSLE measures the average squared logarithmic difference between the predicted and actual values.
    • MSLE treats smaller errors as less significant than larger ones due to the logarithmic transformation.
    • It is less sensitive to outliers than MSE since the logarithmic transformation compresses the error values.

    An example where you can use MSLE –

    Here if you use MSE then due to the exponential nature of the target, it will be sensitive to outliers and MSLE is a better metric, remember that MSLE cannot be used for optimisation, it is only an evaluation metric.

    In general, the choice between MSLE and MSE depends on the nature of the problem, the distribution of errors, and the desired behavior of the model. It’s often a good idea to experiment with both and evaluate their performance using appropriate evaluation metrics before finalizing the choice.